D. PENYEDERHANAAN RANGKAIAN LOGIKA
Bagian ini akan membahas cara menyederhanakan
rangkaian logika dengan peta Karnaugh dan secara aljabar.
1.
Penyederhanaan dengan Peta Karnaugh
Untuk menyederhanakan rangkaian logika dengan peta
Karnaugh, dapat dilakukan langkah-langkah berikut.
a.
Buatlah peta Karnaugh. Tuliskan 1 pada sel yang berhubungan dengan hasil yang didapat
pada tabel kebenaran. Sisanya, tuliskan 0.
b.
Perhatikan pada peta Karnaugh. Apakah ada keluaran 1 yang tidak berkelompok?
Jika
ya, keluaran tersebut adalah keluaran 1 yang terisolasi atau terpencil.
C.
Kelompokkan keluaran 1 yang berdekatan.
d.
Kelompokkan oktet, jika ada.
e.
Kelompokkan quad yang belum dikelompokkan, jika ada.
f.
Kelompokkan pasangan yang belum berpasangan, jika ada.
g.
Bentuklah penjumlahan (OR) dari beberapa kelompok tadi.
2. Penyederhanaan secara Aljabar
Sekarang
Anda akan mempelajari SOP (sum of product) dan POS (product of sum) sebagai
bentuk penyederhanaan rangkaian logika secara aljabar. Apa itu POS dan SOP?
Pelajari bagian ini dengan baik.
• SOP
(sum of product)
SOP adalah jumlah dari perkalian, perhatikan
beberapa contoh SOP berikut.
a.
ABC + ABC
b. AB + BC + CD
• POS (product of sum)
POS adalah perkalian dari penjumlahan, perhatikan
beberapa contoh dari POS berikut.
a.
(A + B)(Ā + C)
b.
(A + B+C)(A + B)(C+D)
Metode penyederhanaan rangkaian logika secara
aljabar yang akan dibahas kali ini hanya SOP.
Berikut ini adalah langkah-langkah penyederhanaan
rangkaian logika, bentuk SOP, secara aljabar.
a.
Ubahlah bentuk
aljabar dari rangkaian logika ke dalam bentuk SOP dengan menggunakan aturan De
Morgan dan perkalian dari beberapa bentuk.
b.
Setelah itu,
faktorkan bentuk perkalian dengan menggunakan sifat distributif. Akibatnya,
hasil faktor saling mengeliminasi dan didapat bentuk aljabar rangkaian logika
yang lebih sederhana.
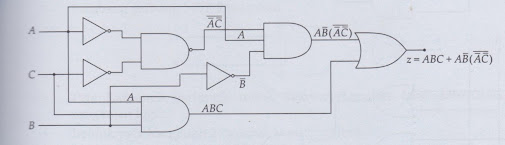
Contoh
Sederhanakan
rangkaian logika berikut.
Pada
rangkaian logika di atas, bentuk aljabarnya, yaitu z = ABC + AB( Ā+C) Bentuk
aljabar tersebut sudah merupakan bentuk SOP, kemudian Anda faktorkan.
z
= ABC + AB( Ā+C) (teorema De Morgan)
=
ABC + AB(A + C) (double inversi)
ABC
+ ABA + ABC = ABC + AB + ABC
=
AC(B +B) + AB = AC + AB (B dan
inversinya saling mengeliminasi)
z
= A(C+B)
Jadi,
bentuk sederhananya adalah z = A(C+B), dan bentuk rangkaiannya sebagai berikut.
Agar Anda lebih paham cara menyederhanakan rangkaian
dengan peta Karnaugh dan aljabar, kerjakan latihan berikut dengan cermat dan
teliti.
•
Keluaran dari gerbang XOR adalah y = ĀB + BA.
•
Lambang gerbang XOR dengan masukan A dan B, yaitu:
•
Gerbang XNOR disebut juga gerbang NOR-eksklusif, yaitu gerbang XOR yang diikuti
oleh sebuah inverter.
•
Keluaran dari gerbang XNOR adalah kebalikan dari keluaran gerbang XOR.
•
Lambang dari gerbang XNOR adalah gerbang XOR yang ditambah sebuah bulatan kecil
yang menandakan inverter seperti berikut.
•
Pada gerbang NAND, masukan-masukan melewati gerbang AND terlebih dahulu sebelum
memasuki inverter.
•
Lambang gerbang NAND
a.
Gerbang NAND 2 masukan
b.
Gerbang NAND 3 masukan
•
Pada gerbang NOR, masukan-masukan melewati gerbang OR terlebih dahulu sebelum
memasuki inverter. Lambang gerbang NOR 2 masukan
•
Peta Karnaugh berfungsi untuk menyederhanakan tabel kebenaran dari suatu
rangkaian logika. • Bentuk peta Karnaugh 2 variabel, seperti berikut.
•
Langkah-langkah penulisan peta Karnaugh:
a.
gambarkan peta Karnaugh,
b.
isi kolom dengan keluaran 1,
c.
isi sisanya dengan 0.
•
Penyederhanaan peta Karnaugh dilakukan dengan cara pengelompokan (pasangan,
quad, oktet), kelompok bertumpang tindih, memutar peta, dan kondisi tak peduli.
Untuk Absen Silahkan klik link dibawah ini :
















0 komentar:
Posting Komentar