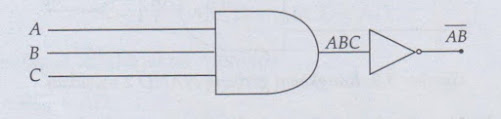
PETA KARNAUGH

 PETA KARNAUGH

Berbagai keadaan dari aljabar Boole biasa dituliskan dalam tabel kebenaran. Semakin banyak variabel maka tabel kebenaran yang ditulis pun semakin besar. Untuk menghemat ruang, digunakan peta Karnaugh bagi tabel kebenaran yang berhubungan. Penyederhanaan tabel kebenaran ini memberikan banyak keuntungan. Salah satu contohnya adalah Anda dapat dengan mudah menelusuri kesalahan gerbang logika karena tampilannya sederhana dan mudah dipahami.

Peta Karnaugh berupa sel sebanyak 2", dengan n adalah banyak variabel dari suatu persamaan Boole. Agar Anda dapat memahaminya, pelajari bahasan berikut.

1. Peta Karnaugh 2 Variabel

Pada persamaan Boole 2 variabel, dibutuhkan sel sebanyak 22 = 4, seperti berikut.

Pada peta Karnaugh 2 variabel terdapat A, A, B, dan B.

·         A menampilkan jika masukan A aktif (1)

·         Ā menampilkan jika masukan A tidak aktif (0)

·         B menampilkan jika masukan B aktif (1)

·         B menampilkan jika masukan B tidak aktif (0)

Misal, terdapat persamaan Boole dengan tabel kebenaran berikut.

 

Berikut ini merupakan langkah-langkah penulisan peta Karnaugh dari tabel kebenaran di atas.

a.       Gambarkan peta Karnaugh

 

b.      Isi kolom dengan keluaran 1

 Kondisi dengan keluaran 1 pada tabel ini ada dua kondisi, yaitu:

A aktif dan B tidak aktif → AB

A aktif dan B aktif → AB

c.       Isi sisanya dengan 0

Jika semua kondisi dengan keluaran 1 telah diisi pada peta Karnaugh, tentu sisanya adalah kondisi dengan keluaran 0.

 

Bentuk tersebut dapat dituliskan dalam hasil kali fundamental berikut.

 y= AB + AB

y= A(B +B)

y = A: 1 y = A

Untuk Absen Silahkan klik link dibawah ini :

https://docs.google.com/forms/d/e/1FAIpQLSe-TztWKislNlC68jy9aNLpeFle62NgXOuNqbaWbj4Y4XLv2A/viewform?usp=sf_link

Read More

Mail Server

 Mail Server

Penggunaan e-mail merupakan sebuah kebutuhan yang tidak dapt dipisahkan dari manusia dalam sektor pekerjaan, bisnis, individu, maupun dunia usaha besar. Dengan semakin berkembangnya teknologi informasi, keberadaan Content Management System (CMS) yang dikhususkan untuk webmail juga makin beragam seperti Zimbra, RoundCube, dan Squirrelmail.

Pada dasarnya, mail server akan melayani para user dalam proses pengiriman dan penerimaan e-mail seperti halnya kantor pos. Selain berfungsi dalam mengirimkan e-mail, mail server juga bertugas untuk menerima e-mail menggunakan protokol POP/IMAP. Salah satu jenis aplikasi POP dan IMAP server yang sering digunakan adalah Courier dan Dovecot. Courier-IMAP merupakan peranti lunak yang digunakan untuk mengambil e-mail yang ada pada mail server. Terdapat perbedaan mendasar antara POP3 dengan mode IMAP. POP3 digunakan untuk pengambilan e-mail dengan cara menghilangkan e-mail yang ada di server, sedangkan pada mode IMAP justru berlaku sebaliknya.

A. Informasi Dasar Mail Server

Mail server merupakan suatu perangkat lunak yang mendistribusikan file atau informasi sebagai balasan atau respons atas permintaan yang dikirim melalui e-mail. Istilah ini juga sering digunakan untuk menunjukkan bitnet yang menyediakan layanan serupa ftp. Tak hanya itu, program ini juga dapat digunakan sebagai aplikasi install e-mail.

1. Pengertian Mail Server

Mail server adalah sebuah server atau layanan internet berbasis cloud computing yang digunakan untuk mengirim dan menerima e-mail dalam satu jaringan mail server yang sama. Mail server dapat mengumpulkan, mengolah, dan mengirim data-data serta informasi dalam bentuk e-mail atau surat elektronik dengan menggunakan domain e-mail khusus atau domain e-mail tersendiri. Mail server menggunakan dasar layanan client-server, di mana client dapat mengakses server e-mail melalui aplikasi. 2. Komponen Mail Server

Komponen mail server penting dimiliki oleh sebuah mail server agar dapat berfungsi maksimal dalam proses menerima dan mengirim e-mail dengan lancar. Pada dasarnya, mail server memiliki tiga aplikasi atau protokol utama, yaitu protokol SMTP (Simple Mail Transfer Protocol), POP3 (Post Office Protocol V3), dan IMAP SMTP, SMTP lebih banyak digunakan untuk menampung data serta mengirimkan e-mail ke alamat e-mail lain yang ingin dituju. Protokol POP3 dan protokol IMAP SMTP lebih banyak digunakan untuk memudahkan user dalam membaca dan mengakses e-mail secara remote.

Selain tiga protokol utama di atas, mail server juga memiliki beberapa hal yang penting sebagai komponen dasar pendukung serta pengoperasiannya. Beberapa komponen yang biasanya dimiliki oleh mail server ada tiga, yaitu MUA (Mail User Agent), MTA (Mail Transport Agent), dan MDA (Mail Delivery Agent).

a. MUA (Mail User Agent)

MUA (Mail User Agent) merupakan program yang digunakan oleh user untuk membaca dan membuat e-mail. Fungsi utama MUA adalah menerima e-mail dan mengirim balasan e-mail. Ada beberapa MUA yang juga dilengkapi dengan Multipurpose Internet Mail Extension (MIME), yaitu program yang digunakan untuk mengirimkan e-mail yang berisi file atau attachment-attachment tertentu.

b. MTA (Mail Transport Agent)

MTA (Mail Transport Agent) adalah salah satu komponen mail server yang bertugas untuk mengurus bagian program pengiriman e-mail. MTA akan melakukan fungsi-fungsi yang harus dilakukannya, yaitu menerima dan memproses

pesan-pesan e-mail yang masuk melalui berbagai macam jaringan, menentukan alamat tujuan sebagai bahan pertimbangan bagaimana cara mengirimkan sebuah pesan e-mail tersebut, serta menggunakan daftar Message distribusi untuk mengirimkan salinan pesan.

 

Gambar 9.1 Mail Transport Agent (MTA)

Sumber: http://my-tiny.net/logos/port587.jpg

C. MDA (Mail Delivery Agent)

MDA (Mail Delivery Agent)merupakan bagian program dari mail server yang bertugas sebagai agen pengiriman pesan e-mail. MDA memiliki dua komponen utama, yaitu sebuah database yang berisi saluran atau jaringan untuk mengirimkan pesan serta delivery agent yang bertugas untuk mengirimkan pesan e-mail sesuai dengan jaringan yang dipilih.

Link Absen :

https://docs.google.com/forms/d/e/1FAIpQLSdMQeASbkoxHdutPnmqoUnB3uYvuwhN3-p4-zO42zeBXF18mQ/viewform?usp=sf_link

 

Read More

B. GERBANG NAND DAN NOR

 

B. GERBANG NAND DAN NOR

Pada bagian sebelumnya, telah Anda ketahui bahwa gerbang XNOR merupakan gerbang EXOR yang diberi inverter. Berbeda dengan EXOR dan XNOR, gerbang NOR dan gerbang NAND tidak berkaitan. Pada gerbang NAND, masukan memasuki gerbang AND terlebih dahulu, kemudian memasuki inverter. Sementara itu, pada gerbang

inverter.

1. Gerbang NAND Gerbang NAND 2 masukan

Gambar 3.9 Rangkaian gerbang NAND 2 masukan

Pada gambar di atas terdapat 2 masukan yang terhubung oleh gerbang AND. Kemudian, keluaran dari gerbang AND tersebut melalui sebuah inverter. Berikut adalah empat kondisi dari gerbang NAND.

1) Kondisi 1

A = 0 dan B = 0

y = (0 : 0)' = 0' = 1

2) Kondisi 2

A = 1 dan B = 0

y = (1 : 0)' = 0' = 1

Kondisi 3

 A = 0 dan B = 1

y = (0 - 1)' = 0' = 1

Kondisi 4

A = 1 dan B = 1

y = (1 · 1)' = 1' = 0

Dari empat kondisi tersebut, didapat tabel kebenaran dan diagram pewaktuan berikut.

Tabel 3.3 Tabel Kebenaran NAND 2 Masukan

 

Gambar 3.10 Diagram pewaktuan gerbang NAND 2 masukan

Contoh di atas adalah gerbang NAND untuk 2 masukan. Bagaimana gerbang NAND untuk 3 masukan? Perhatikan gambar berikut.

 

Gambar 3.11 Rangkaian gerbang NAND dengan 3 masukan

Pada gambar di atas, 3 masukan yakni ABC memasuki gerbang AND, kemudian keluarannya melewati inverter menghasilkan ABC .

Tabel 3.4 Tabel Kebenaran Gerbang NAND 3 Masukan

 

Gambar 3.12 Diagram pewaktuan gerbang NAND 3 masukan

2. Gerbang NOR

Gerbang NAND adalah gerbang AND yang diikuti oleh inverter, sedangkan gerbang NOR adalah gerbang OR yang diikuti oleh inverter, perhatikan gambar berikut.

 

Gambar 3.13 Gerbang NOR

Pada gerbang NOR di atas, terdapat 2 masukan, A dan B, yang terhubung oleh sebuah gerbang OR. Keluaran dari gerbang OR tersebut melalui sebuah inverter. Jadi, didapat beberapa kondisi untuk 2 masukan gerbang NOR.

a.    Kondisi 1

 A = 0 dan  B = 0

y = (A + B)' = (0+ 0)' = 0' = 1

b.      Kondisi 2

 A = 1 dan B=0

y = (A + B)' = (1 + 0)' = 1' = 0

c.       Kondisi 3

 A = 0 dan B = 1

y = (A + B)' = (0 + 1)' = 1' = 0

d.   Kondisi 4

A = 1 dan B = 1

y = (A + B)' = (1 + 1)' = 1' = 0

Dari empat kondisi tersebut, didapat tabel kebenaran dan diagram pewaktuan berikut.

Tabel 3.5 Tabel Kebenaran Gerbang NOR

 

Gambar 3.14 Diagram pewaktuan gerbang NOR

Coba Anda gambarkan lambang dari gerbang NOR dengan masukan 3 variabel, ABC. Kemudian, buat tabel kebenaran dan diagram pewaktuannya.

 

Untuk Absen Silahkan klik link dibawah ini :

https://docs.google.com/forms/d/e/1FAIpQLSe-TztWKislNlC68jy9aNLpeFle62NgXOuNqbaWbj4Y4XLv2A/viewform?usp=sf_link

Read More

Menu dan ikon pada program CorelDRAW X7

 

6. Menu dan ikon pada program CorelDRAW X7

 a. Menu bar

Pada menu bar CorelDRAW X7, terdapat dua belas menu standar. Menu tersebut, antara lain

File, Edit, View, Layout, Arrange, Effects, Bitmaps, Text, Table, Tools, Window, dan Help.

Oleh karena hampir semua menu pada menu bar mempunyai peran yang sama penting, pelajari menu dan submenu CorelDRAW X6 berikut.

1) Menu File

Menu File merupakan menu yang letaknya paling ujung kiri pada menu bar CorelDRAW X7. Pada menu ini terdapat submenu beserta fungsinya sebagai berikut.

 SubmenuFungsi

New                            :Membuka file baru yang masih kosong (Ctrl+N)

New From Template   :Membuka file baru dari desain template yang disediakan CorelDRAW

Open                           :Membuka file yang pernah dibuat (Ctrl+O)

Close                           :Menutup file

Close All                     :Menutup keseluruhan lembar kerja

Save                            :Menyimpan file desain grafis yang dibuat (Ctrl+S)

Save As                       :Menyimpan file desain dengan nama yang baru (Ctrl+Shift+S)

Revert                         :Kembali ke pertama kali sebelum disimpan

Acquire Image                        :Memberi efek image

Import                         :Mengambil gambar dari file lain (Ctrl+1)

Export                         :Mengirim gambar ke program lain (Ctrl+E)

Send To                        :Mengirim gambar untuk dibuat desktop atau untuk disimpan didrive tertentu

Print                            :Mencetak hasil gambar (Ctrl+P)

Print Merge                 :Mencetak desain grafis yang telah dibuat

Print Preview              :Melihat perkiraan hasil gambar pada layar sebelum dicetak

Print Set Up                :Mengatur hasil cetakan

Publish To PDF           :Menyimpan halaman ke bentuk PDF

Publish Page To Conceptshare            :Menyimpan halaman ke halaman web

Document Properties  :Meminta informasi tentang suatu dokumen

Opent Recent              :Membuka file grafis yang pernah dibuka

Exit                             :Keluar dari program CorelDRAW X7 (Alt+F4)

2) Menu Edit

Kelompok menu Edit ini berhubungan dengan penyuntingan (editing) teks maupun gambar. Menu ini terdiri atas submenu seperti berikut.

Undo               : Fungsi Membatalkan perintah yang dilakukan (Ctrl+Z)

Redo               : Mengembalikan perintah sebelumnya (Ctrl+Shift+Z)

Cut                    : Memotong sebuah objek atau teks yang dipilih atau disorot ke clipboard (Ctrl+X)

Copy               : Menyalin teks atau objek yang dipilih atau disorot ke clipboard (Ctrl+C)

Paste                  : Menempatkan teks atau objek yang ada di clipboard pada posisi titik sisip berada (Ctrl+V).

Paste Special   : Menempatkan teks atau objek yang ada di clipboard pada posisi titik sisip berada, tetapi dengan format yang berbeda

Delete Symbol            : Menghapus teks atau objek yang diblok atau ditandai

Duplicate         : Menyisipkan simbol ke dalam lembar kerja Membuat duplikat atau salinan objek saat itu juga (Ctrl+D)

Select All        : Melakukan seleksi (pilihan) untuk semua teks atau objek

Find and Replace        :Mencari dan mengganti objek

Insert Barcode            :Menyisipkan barcode ke dalam lembar kerja

Insert New Object      :Membuat objek dari program lain lalu menempatkan objek itu pada

program CorelDRAW X7 |

Properties        :Menampilkan keterangan seputar teks atau objek yang sedang aktif

Kelompok menu View ini berhubungan dengan pengaturan jendela kerja suatu dokumen. Menu ini mempunyai submenu seperti berikut.

 

Silahkan Untuk Absen :

https://docs.google.com/forms/d/e/1FAIpQLSe19Bl0Zr4JrvQ8-b6iPJrhSrxeVWtmAudvyschyixkF5NyCw/viewform?usp=sf_link

 

Read More

Instalasi Dan Konfigurasi database server

 

0. Selanjutnya, sistem melakukan update hak akses (privilege) menggunakan

tabel yang ada di database sehingga sistem akan memberikan konfirmasi untuk mengizinkan prosedur update hak akses dari tabel dengan memberikan pernyataan reload privilege tables now. User dapat menekan tombol Enter secara langsung untuk melanjutkan tahap berikutnya.

 

Gambar 8.20 Konfirmasi update hak akses tabel dalam database

Sumber: https://dc392.4shared.com/img/NnOu3f7eeel$23/16694eb17d8/bb8mr17

P. Jika tahap reload privilege tables now selesai dikerjakan, menandakan bahwa sistem akan menerapkan semua perubahan yang ada di dalam database tersebut. Pada tahap ini, MariaDB Server sudah dapat digunakan.

 

Gambar 8.21 Sistem melakukan penerapan konfigurasi ke database server

Sumber: https://dc614.4shared.com/img/mrMsx16mee/ $23/16694eb2390/bb8mr18

2. Uji Coba MariaDB Server dengan Aplikasi PhpMyAdmin

Hal mendasar yang perlu dipahami dalam melakukan uji coba semua service server yang ada di server Linux Debian adalah user “phpmyadmin” tidak dapat digunakan untuk membuat, menghapus, dan mengedit sebuah database. Langkahlangkah dalam melakukan uji coba database server dengan aplikasi PhpMyAdmin adalah sebagai berikut. a. Diawali dengan mengaktifkan Mozilla Firefox atau web browser lain yang sejenis.

a.    Setelah itu, di kolom URL ketikkan alamat server disertai path"/phpmyadmin”. Misalnya 192.168.100.1/phpmyadmin dan diakhiri dengan menekan tombol Enter atau klik icon Go (7) di pojok kanan sehingga muncul hasil tampilan gambar sebagai berikut.

 

Gambar 8.22 Tampilan menu login aplikasi PhpMyAdmin

Sumber: https://dc614.4shared.com/img/RCoDziDTda/ $23/16694eb2b60/bb8mr18b

b. Setelah itu, mengisi user dengan PhpmyAdmin dan password-nya sesuai dengan yang sudah konfigurasi sebelumnya. Jika sudah, silahkan klik menu Go untuk masuk ke dalam database server.

 

Gambar 8.23 Login ke dalam aplikasi

Sumber: https://dc392.4shared.com/img/Yze63z0egm/ $23/16694eb3718/bb8mr19 158 Aam

c.    Jika login dan kata sandi (password) yang dimasukkan sudah benar maka user akan dibawa masuk ke dalam sistem database server sebagai berikut.

 

Gambar 8.24 Tampilan database server di lihat dari aplikasi PhpMyAdmin

Sumber: https://dc392.4shared.com/img/l_0EaMnheel $23/16694eb42do/bb8mr20

Info

Database Warehouse Database Warehouse (DW atau DWH) juga dikenal sebagai Enterprise Data Warehouse (EDW), adalah sistem database yang digunakan untuk pelaporan dan analisis data, serta dianggap sebagai komponen inti dari business intelligence. Database Warehouse (DW) adalah gudang data terpadu, terdiri atas satu atau beberapa sumber yang berbeda. Databasemenyimpan data terkini dan historis di satu tempat dan digunakan untuk membuat laporan analisis.

Sumber: http://www.pintarkomputer.org/2017/11/macam-macam-database-lengkap-dan.html

Rangkuman

1. Database server merupakan sebuah program komputer yang menyediakanlayanan pengelolaan basis data dan melayani komputer atau program aplikasi basis data dengan menggunakan model client atau server.

2. Catatan yang mirip dengan basis data sebenarnya sudah ada sebelum revolusi industri, yaitu dalam bentuk buku besar, kuitansi, serta kumpulan data yang berhubungan dengan dunia usaha atau bisnis.

3. Oracļe dikenal sebagai database server untuk internet dan jaringan sekaligus sebagai salah jenis Relational Database Management System (RDBMS) dalam mengelola informasi secara terbuka, komprehensif, dan terintegrasi.

4. Microsoft SQL Server adalah peranti lunak Relational Database Management System (RDBMS) yang didesain untuk melakukan proses manipulasi database berukuran besar dengan berbagai fasilitas.

5. PostgreSQL merupakan sebuah Object-Relational Database Management System (ORDBMS) berdasarkan pada PostgreSQL Versi 4.2

6. PhpMyAdmin adalah suatu aplikasi berbasis PHP (Hypertext Preprocessor) yang berguna untuk pengelolahan administrasi database MySQL berbasis GUI melalui World Wide Web (www).

Link Absen :

https://docs.google.com/forms/d/e/1FAIpQLSdMQeASbkoxHdutPnmqoUnB3uYvuwhN3-p4-zO42zeBXF18mQ/viewform?usp=sf_link

 

Read More

Gerbang XNOR

 

2. Gerbang XNOR

Gerbang XNOR disebut juga gerbang NOR-eksklusif, yaitu gerbang EXOR yang diikuti oleh sebuah inverter. Berikut merupakan rangkaian gerbang XNOR.

 

Gambar 3.4 Rangkaian gerbang XNOR

Gambar di atas menunjukkan sebuah gerbang XNOR dengan 2 masukan, A dan B. Masukan A dan B dihubungkan oleh sebuah gerbang EXOR. Kemudian, keluaran dari gerbang EXOR tersebut dibalik oleh sebuah inverter. Inverter biasa dilambangkan dengan sebuah lingkaran kecil. Karena XNOR kebalikan dari EXOR maka lambang dari XNOR adalah lambang EXOR yang ditambah dengan sebuah lingkaran kecil yang menandakan inverter.

 

Gambar 3.5 Penyederhanaan rangkaian XNOR

Berikut ini merupakan tabel kebenaran dan diagram pewaktuan gerbang XNOR.

Tabel 3.2 Tabel Kebenaran XNOR

 

 

Gambar 3.6 Diagram pewaktuan gerbang XNOR

3. Implementasi Gerbang EXOR dan XNOR

 Gambar 3.7 Contoh rangkaian logika dengan gerbang EXÖR dan gerbang XNOR

Rangkaian di atas jika disederhanakan, dapat diubah menjadi beberapa gerbang XOR dan XNOR.

Ingat bahwa untuk gerbang XOR, y = AB + BA. Adapun gerbang XNOR merupakan negasi dari XOR yang ekivalen dengan persamaan y = AB + AB.

Rangkaian di atas dapat disederhanakan dengan aljabar, berikut keluaran dari rangkaian tersebut.

z = ABCD + ABCD+ ĀD

Persamaan di atas dapat difaktorkan menjadi

z = AD(BC + BC) + ĀD

Jika persamaan yang lebih sederhana tersebut digambarkan dalam bentuk rangkaian logika maka akan menjadi seperti berikut.

Kerjakan Soal Latihan Berikut

Untuk Absen Silahkan klik link dibawah ini :

https://docs.google.com/forms/d/e/1FAIpQLSe-TztWKislNlC68jy9aNLpeFle62NgXOuNqbaWbj4Y4XLv2A/viewform?usp=sf_link

Read More

Lanjutan Instalasi MariaDB Server

h. Langkah berikutnya adalah melakukan konfigurasi user root untuk database server. Hal mendasar yang perlu diingat adalah user root sebagai user tertinggi Perintah yang digunakan untuk melakukan konfigurasi user root adalah mysql secure_instalation. Selanjutnya, tekan tombol Enter untuk melanjutkan proses instalasi.

 

Gambar 8.13 Perintah melakukan setup database server

Sumber: https://dc392.4shared.com/img/7CLJqYolda/ $23/16694ead188/bb8mr10

i.      Selanjutnya, menentukan password untuk user root di database server. Oleh karena belum melakukan konfigurasi apa pun maka user dapat langsung saja menekan tombol Enter untuk menuju tahap selanjutnya.

Gambar 8.14 Menentukan password root untuk database

server Sumber: https://dc.14.4shared.com/img/_h67A3KDeel $23/16694ead570/bb8mr1

j.  Sistem secara otomatis memberikan tampilan konfirmasi “set root password? (Y/n)”. Tampilan tersebut dapat diisi dengan mengetik huruf“Y” terlebih dahulu dilanjutkan dengan menekan tombol Enter yang ada pada keyboard untuk melanjutkan proses instalasi."

Gambar 8.15 Konfirmasi untuk membuat password untuk user root database

Sumber: https://dc614.4shared.com/img/ PjbOk5V5ee/s23/16694eae128/bb8mr12Set root password? [Y/n] Y

k. Langkah selanjutnya, memasukkan kata sandi (new password) dan verifikasi kata sandi (re-enter password) untuk user root di database server yang baru. Guna mengakhiri proses pembuatan password tekan tombol Enter yang ada pada keyboard. 

Gambar 8.16 Menentukan password user root database server

Sumber: https://dc392.4shared.com/img/IDT7pW0Qgm/ $23/16694eae8f8/bb8mr13

1.      Setelah itu, sistem akan memberikan konfirmasi untuk menghapus Anonymous user. Secara langsung pengguna dapat menekan tombol Enter untuk melanjutkan langkah berikutnya. 

Gambar 8.17 Menghapus Anonymous user pada database server

Sumber: https://dc392.4shared.com/img/x-ljlryegm/ $23/16694eaf898/bb8mr14

m. Selanjutnya, menentukan pilihan "disallow root login remotely” yang melarang user root untuk login menggunakan metode remote. User dapat secara langsung menekan tombol Enter untuk melanjutkan langkah berikutnya.

Gambar 8.18 Konfigurasi melarang user root login via remote

Sumber: https://dc392.4shared.com/img/ywpmQ4oXfi/$23/16694eb0068/bb8mr15

n. MariaDB server secara default melakukan instalasi dan membuat database bernama test. Oleh sebab itu, sistem akan meminta konfirmasi untuk menghapus database tersebut. Secara langsung, user dapat saja menekan tombol Enter untuk melanjutkan langkah berikutnya. Activities Terminal

Gambar 8.19 Konfirmasi untuk menghapus database bernama "test"

Sumber: https://dc614.4shared.com/img/9R3NU2Vsfi/ $23/16694eb1008/bb8mr16

 Link Absen :

https://docs.google.com/forms/d/e/1FAIpQLSdMQeASbkoxHdutPnmqoUnB3uYvuwhN3-p4-zO42zeBXF18mQ/viewform?usp=sf_link

 

Read More